[데이터베이스] Relational Database Design (2)

• Golas of Normalization
  1. each relation scheme is in good form
  2. the decomposition is a lossless-join decomposition
  3. preferably, the decomposition should be dependency preserving.

이전 글에서 배웠던 closure of functional dependency 에 대한 예를 보자

cf. reflexivity, augmentation, transitivity, union, decomposition, pseudotransitivity

 

ex ) R = { A, B, C, G, H, I } 

F = { A->B, A->C, CG->H, CG->I, B->H } 가 있다고 할때

 

F+를 몇 개 더 구해보자

A->H >> A->B 이고 B->H 이므로 transitive 속성으로 A->H 인 것을 추가적으로 알 수 있다.

AG->I >> A->C 이므로 augmentation 속성으로 AG->CG 이고 따라서 CG->I 이므로 transitivity속성으로 AG->I인 것도 알 수 있다.

CG->HI >> CG->I 의 augmentation 속성으로 CG->CGI 인것을 알 수 있고 CG->H 는 augmentation 속성으로 CGI->HI 인 것도 알 수 있다. 따라서 CG->CGI , CGI->HI 이므로 transitivity 속성을 이용해 CG->Hi 인것까지 구해낼 수 있다.

 

F+를 구하는 알고리즘을 간략하게 말하면 우선 reflexivity 와 augmentation의 속성들을 다 찾아서 더한 후에

transitivity의 속성을 원래 F와 추가된 속성에서 찾아내서 더이상의 f+에 덜할 것이 없을때까지 반복문을 돌리는 것이다.

attribute가 n개 라면 2^2n의 개수가 나올수 있어 알고리즘 수행시간은 O(2^n)이다.

 

이때까지 했던 것은 "Closure of Functional Dependency" 였다. 이제 "Closure of Attribute Sets"에 대해서 알아보자.

 

attribute set이 a 라고 한다면 a로 부터 도달할 수 있는 모든 것들을 a+라고 한다.

예) R = { A,B,C} // F = {A->B, B->C}라고 한다면 A+는 {A,B,C} 인 것이다. 

이때 a+가 R가 똑같다면 a 는 그 relation의 key 라고 한다!

 

이것에 대한 알고리즘은 간략하게 말하자면 a 로 부터 도달 가능한 것들을 result라고 하고 a를 먼저 result 에 넣어준다. 반복문을 돌 때 b가 현재 result에 있고 b->r의 관계를 발견한다면 result에 r도 추가시키는 것이다. 이것의 수행시간은 n+n-1+,,+1 = O(n^2) 이다.

 

ex) R = ( A,B,C,G,H,I ), F = { A->B, A->C, CG->H, CG->I, B->H }

(AG)+ 는

1. result = AG

2. result = ABCG ( A->C and A->B )

3. result = ABCGH ( CG->H and CG는 AGBC 에 속한다. )

4. result = ABCGHI ( CG->I and CG는 AGBCH 에 속한다.)

AG는 candidate key 인가 >> super key 는 맞으나 A와 G 각각이 key 가 아니라면 candidate key 의 조건 까지 만족한다.

 

Attribute Closure 를 사용하는 것은 슈퍼 키인지 판단하거나 Functional dependencies를 만족하는지 판단 할 때 사용한다.

 

Lossless-join Decomposition

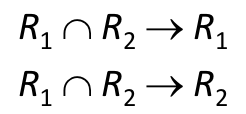
Lossless-join을 만족시키려면 위의 사진처럼 둘 중 하나의 조건은 만족해야한다.

만약 r( A, B, C, D) 라면 (A,B)//(C,D) 이렇게 는 분해 할 수 없다. 

(A,B)//(A,C,D) -->> 이렇게 decomposition을 하고 A 가 R1 가 R2에서 key의 역할을 하고 있어야한다ㅏ.

첫 번째 분해 시에 (A,B) 와 (B,C) 로 하면 R1과 R2의 교집합인 B이고 B는 R2에 속하기 때문에 Lossless를 보장하고 있다.

추가적으로 FD를 각각의 relation을 join 하지 않고 각각으로 검사가 가능하기 때문에 Dependency preserving 또한 보장된다.

하지만 B->R 이 아닌 상태에서 키의 역할을 하고 있기 때문에 BCNF는 아니다.

 

두 번째 분해는 (A,B) (A,C)로 하면 두 테이블의 교집합인 A가 R1에 속하기 때문에 lossless는 보장한다.

추가적으로 각각의 릴레이션을 조인하지 않고 FD를 검사하는 것은 불가능하기 때문에 Dependency preserving은 보장하지 않는다.

마지막으로 두 relation의 key인 A가 A->R이기 때문에 BCNF는 만족한다.

 

Dependency Preservation

Ri 의 FD 를 Fi 라고 할 때, DP가 보장된다는 것은

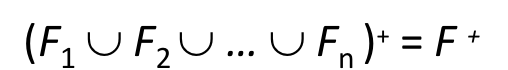
위 사진의 조건을 만족한다는 것이다. 즉 각각의 릴레이션에 대한 functional dependency를 모으면 F+가 만들어진다는 것.

만약 DP가 보장이 안된다면 = 이 아닌 ⊆ 의 형태일 것이다.

위의 사진을 설명하자면 JK->L 이므로 JK->JKL 따라서 JK->R 이다. 즉 JK 는 이 릴레이션의 KEY이다.

또한 L->K, JL->JK, JL->JKL의 과정을 거쳐서 JL->R인 것을 확인할 수 있어 JL도 이 릴레이션의 KEY이다. 

KEY = [J,K] 로 L->K의 조건때문에 L 은 KEY가 아닌데 왼쪽에 위치하여 이 릴레이션은 BCNF가 아닌 것을 알 수 있다.

Decomposition을 해야하므로 L->K의 조건으로 a->b 일때 a교집합b 와 R-(b-a)로 분해하면

R1=(J,L) R2=(L,K)로 분해된다. 이때 key 들이 fd의 왼쪽에 위치하고 있기에 BCNF 이지만 조인을 하지 않고서는 FD를 검사할 수 없기 때문에 DP를 만족한다고 볼 수 없다.

따라서 분해 전의 상황을 보면 r(J,K,L) 일때 JK->L L->K 일때  JK->K transitivity 속성을 이용한 것이 아니기때문에 3NF는 만족한다고 볼 수 있다.

 

📌BCNF : lossless 만족, key들은 FD의 왼쪽에 있어야함, DP는 보장되지 못할 수도 있다

📌3NF : lossless 만족, DP 만족, transitivity 속성은 만족하지 않아야함.